Given data:
The expression for length of rectangle is l=w+20.
The area of rectangle A=2400 square-yards.
The expression for the area of area of rectangle is,
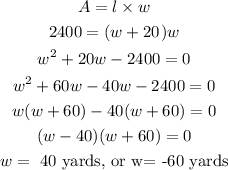
As the side of the rectangle can't be negative, so width is 40 yards.
The length of rectangle is,
l=(40+20) yards
=60 yards.
Thus, the width of rectangle is 40 yards and length is 60 yards, the mistake made by the student he took width 60 yards but it is not possible.