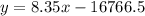Given the points
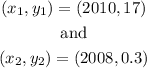
we will find the slope m and the y-intercept b.
The slope m is given as
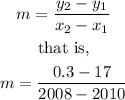
which gives
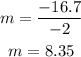
Then, the line equation in slope-intercept form is
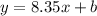
In order to find the y-intercept b, we can substitute one of the given point, for instance, by replacing point (2010,17) in the last result, we have
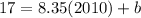
which gives
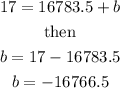
Then, the answer is