Question

A rectangle has a length of 4' and a perimeter of 14'. What is the perimeter of a similar rectangle with a width of 9'?

Answer 1

G. 42 feet

Explanation:

Given:

L1 = 4 ft

P1 = 14 ft

W2 = 9 ft

We know that the perimeter is the sum of all the sides. With this we can calculate the width of the first rectangle, like this:

`\begin{gathered} P_1=L_1+L_1+W_1+W_1 \\ 2\cdot W_1=P_1-2L_1 \\ W_1=(P_1-2L_1)/(2) \\ \text{we replacing} \\ W_1=(14-2\cdot4)/(2)=(14-8)/(2)=(6)/(2) \\ W_1=3\text{ ft} \end{gathered}`

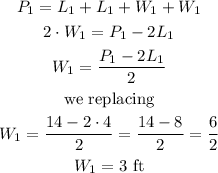
Since they are similar, we can calculate the ratio between rectangles, calculating the ratio between widths like this:

`r=\frac{W_2}{W_1_{}}=(9)/(3)=3`

We can calculate the length of the second rectangle with the help of the ratio, just like this:

`\begin{gathered} r=(L_2)/(L_1) \\ L_2=r\cdot L_1=3\cdot4 \\ L_2=12\text{ ft} \end{gathered}`

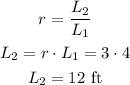
Therefore, now if we can calculate the perimeter of the second rectangle:

`\begin{gathered} P_2=L_2+L_2+W_2+W_2 \\ \text{ we replacing} \\ P_2=12+12+9+9 \\ P_2=42\text{ ft} \end{gathered}`

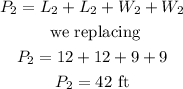
Therefore the perimeter of the similar rectangle is 42 feet.