Given
z varies directly as x². If z = 18 when x = 3.
To find z, when x = 4.
Step-by-step explanation:
It is given that,
z varies directly as x².
That implies,
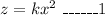
Since z=18, when x=3.
Then,
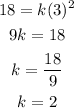
Therefore, (1) becomes,
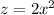
Also, for x=4,
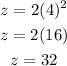
Hence, the value of z is 32 when x=4.