Question

Peter invested some money at 6% annual interest, and Martha invested some at 12%. If their combined investment was $6,000 and their combined interest was $570, how much money did Martha invest? $

Answer 1

The annual interest is determined using the following formula:

`A=P* i* t`

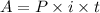
Where "A" is the interest, "i" the interest rate in decimal notation and "t" represents time. "P" is the amount invested:

Since the combined interest is $570:

`P_P* i_P* t_{}+P_M* i_M* t=570`

And since the combined investment was $6000 we have:

`P_P+P_M=6000`

Solving for the amount invested by Martha:

`P_P=6000-P_M`

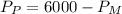
replacing in the formula for the interest:

`(6000-P_M)* i_P* t_{}+P_M* i_M* t=570`

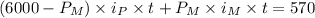
Replacing the known values:

`(6000-P_M)*(0.06)* t_{}+P_M*(0.12)* t=570`

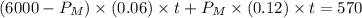
Simplifying:

`360t-0.06P_Mt+0.12P_Mt=570`

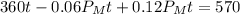
Now we solve for the amount invested by Martha:

`\begin{gathered} -\text{0}.06P_Mt+0.12P_Mt=570-360t \\ P_M(-0.06t+0.12t)=570-360t \\ P_M=(570-360t)/(-0.06t+0.12t) \end{gathered}`

Since we are not given the amount of time "t", we can't determine the exact value of the amount invested by Martha.