We are told that the ratios between areas of two circles are 9 to 16, this means the following:
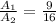
Since the area of a circle is given by the following formula:

Replacing in the proportion:
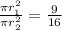
canceling out the pis:
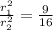
Now we use the following property of exponents:
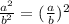
Applying the property:

Now we take the square root to both sides:
![(r_1)/(r_2)=\sqrt[]{(9)/(16)}](https://img.qammunity.org/2023/formulas/mathematics/college/me9noaiaczu9wkk0nbahnbydwux5h123id.png)
Solving:

Therefore, the radius is at a proportion of 3 to 4.