Question

OpFind the volume of the cone. Round your answersto the nearest tenth37.7 in33393 in113.1 in

Answer 1

For this problem we are given the height of a cone, and the diamater of its base. From this information, we need to determine the volume of the cone.

The volume of a cone is given by the following formula:

`V=\pi\cdot r^2(h)/(3)`

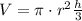
The radius of the base is half the diameter, so we can determine the radius from the given information, as shown below:

`\begin{gathered} r=(d)/(2) \\ r=(6)/(2)=3 \end{gathered}`

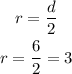
We can now use the formula for the volume.

`\begin{gathered} V=\pi\cdot(3)^2\cdot(12)/(3) \\ V=\pi\cdot9\cdot4 \\ V=113.04\text{ cubic inches} \end{gathered}`

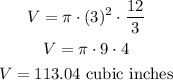
The volume