b.
To determine the half life we plug half the original amount in the expression given and solve for t:

Therefore the half-life of the substance is approximately 154 years.
c.
To determine how much of the substance will be after 2500 years we just plug this value in the expression:
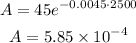
Therefore after 2500 years there will be:
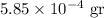
of the substance.