Question

Given the function h(x)=-x^2+10x+32, determine the average rate of change of the function over the interval 3≤x≤11.

Answer 1

-4

Explanation:

Write the function as an equation.

`y=-x^(2)+10x+32`

Substitute using the average rate of change formula.

The average rate of change of a function can be found by calculating the change in y values of the two points divided by the change in x values of the two points.

`(f(11)-f(3))/((11)-(3))`

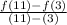
Substitute the equation
`y=-x^(2)+10x+32` for
`f(11)` and
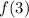`f(3)`, replacing

x in the function with the corresponding x value.

`((-(11^(2))+10(11)+32)-(-(3)^(2) +10(3)+32 )/((11)-(3))`

After some painful algebra the expression can be simplified to
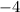`-4`.