Question

See attached Question, part cangular velocity (part A): 0.136 rad/s

Answer 1

Before the collision, the only moving element on the system was the disk, which has a mass of 52.0g and a speed of 35.0m/s. Then, the linear momentum of the system before the collision is:

`\begin{gathered} p=mv \\ =(52.0g)(35.0(m)/(s)) \\ =(0.0520kg)(35.0(m)/(s)) \\ =1.82kg(m)/(s) \end{gathered}`

Therefore, the linear momentum of the system before the collision, is: 1.82 kg*m/s.

After the collision, both the disk and the stick rotate with an angular speed of 0.136 rad/s.

We can consider the mass of the stick as if it was a particle with the same mass located at the center of mass of the stick, which is halfway between the ends of the stick.

The linear momentum of the system can be calculated as:

`P=Mv_M+mv_m`

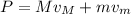
The tangential speed of a point located a distance r from the axis of rotation, when it is rotating at an angular speed ω, is:

`v=\omega r`

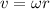
Then, the velocities of the particle that represents the stick and the disk are:

`\begin{gathered} v_M=\omega\cdot(L)/(2) \\ \\ v_m=\omega d \end{gathered}`

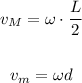
Where L is the length of the stick and d is the distance from the disk to the nail. Then, the linear momentum in terms of known variables is:

`\begin{gathered} P=Mv_M+mv_m \\ \\ =M\cdot(\omega L)/(2)+m\cdot\omega d \\ \\ =\left((ML)/(2)+md\right)\omega \end{gathered}`

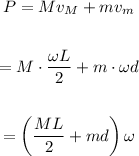
Replace ω=0.136 rad/s, L=1.40m, M=2.05kg, m=0.0520kg and d=0.100m:

`\begin{gathered} P=\left((ML)/(2)+md\right)\omega \\ \\ \\ =\left(((2.05kg)(1.40m))/(2)+(0.0520kg)(0.100m)\right)\left(0.136(rad)/(s)\right) \\ \\ =0.1958...kg\cdot(m)/(s) \\ \\ \therefore P\approx0.196\,kg\cdot(m)/(s) \end{gathered}`

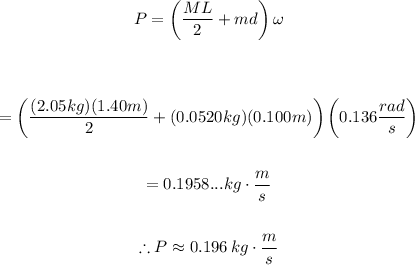
Then, the linear momentum after the collision is approximately 0.196 kg*m/s.