Question

You invested money in two funds. The first fund paid a dividend of 9% and the second 3%. You received 879. This year the fund paid 10% and 1% and you received 853. How much money did you invested in each fund?

Answer 1

The given information is:

- Last year you received a total of $879.

- The first fund paid a dividend of 9% and the second fund paid a dividend of 3%.

- This year you received a total of $853.

- The first fund paid a dividend of 10% and the second fund paid a dividend of 1%.

We can make an equation for the money you received each year.

Let's set x=money you invested in the first fund and y=money you invested in the second fund.

Then, last year dividend's equation is:

`x*0.09+y*0.03=879\text{ Equation 1}`

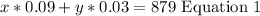
Now, for this year the equation will be:

`x*0.10+y*0.01=853\text{ Equation 2}`

Let's isolate y from equation 2:

`\begin{gathered} 0.10x+0.01y=853 \\ 0.01y=853-0.10x \\ y=(853-0.10x)/(0.01) \end{gathered}`

Now, replace y into equation 1 and solve for x:

`\begin{gathered} 0.09x+0.03((853-0.10x)/(0.01))=879 \\ \\ 0.09x+3(853-0.10x)=879 \\ 0.09x+2559-0.30x=879 \\ -0.21x=879-2559 \\ -0.21x=-1680 \\ x=(-1680)/(-0.21) \\ \\ x=8000 \end{gathered}`

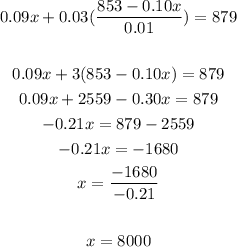
Replace x into y-equation and solve:

`\begin{gathered} y=(853-0.10*8000)/(0.01) \\ \\ y=(853-800)/(0.01) \\ \\ y=(53)/(0.01) \\ \\ y=5300 \end{gathered}`

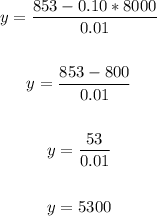
So, x=8000 and y=5300.

You invested $8000 in the first fund and $5300 in the second fund.