We are given the following two functions

Recall that the rule for reflection over the y-axis is given by
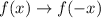
As you can see, the graph of g(x) will be a reflection over the y-axis of the graph f(x).
Recall that the rule for vertical translation (upward) is given by
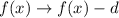
The above translation will shift the graph vertically upward by d units.
For the given case, d = 1
As you can see, the graph of g(x) will be a vertical translation of the graph f(x)
Therefore, we can conclude that the graph of g(x) will be a reflection over the y-axis and a vertical translation of the graph f(x).
1st option is the correct answer.