Given:
The mass of the automobile is m = 1060 kg
The speed of the automobile is

Required:
(a)The kinetic energy
(b) Work done to bring the automobile to stop.
Step-by-step explanation:
(a) The kinetic energy can be calculated by the formula
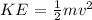
On substituting the values, the kinetic energy will be
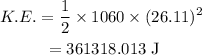
(b) Work done is defined as the change in kinetic energy.
To stop the automobile, the kinetic energy should be zero.
So, the work done can be calculated as
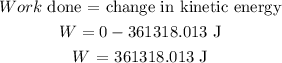
Final Answer:
(a)The kinetic energy is 361318.013 J
(b) Work done to bring the automobile to stop is 361318.013 J