Question

The greatest of three numbers is six times the smallest, and the middle number is 10 more than the smallest. If twice the greatest is decreased by 90 the result is the sum of the middle in the smallest. find the three numbers.

Answer 1

We are gonna call x the greatest number, y is the middle number and z is the smallest number.

"The greatest of three numbers is six times the smallest" is expressed as

`x=6z`

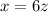
"The middle number is 10 more than the smallest" is expressed as

`y=10+z`

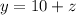
"Twice the greatest is decreased by 90 the result is the sum of the middle and the smallest" is expressed as

`2x-90=y+z`

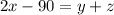
First, we replace the first equation into the third one

`\begin{gathered} 2(6z)-90=y+z \\ 12z-90=y+z \\ -90=y+z-12z \\ -90=y-11z \end{gathered}`

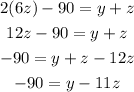
Now, we replace the second equation into the last one above

`\begin{gathered} -90=10+z-11z \\ -90-10=-10z \\ -100=-10z \\ z=(-100)/(-10)=10 \end{gathered}`

Then, we find x

`x=6(10)=60`

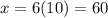
We find y

`y=10+z=10+10=20`

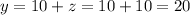
Therefore, the greatest number 60, the middle number is 20 and the smallest number is 10.