Question

Can you please help me out with a question

Answer 1

Step 1

Write the expression for the surface area of a hemisphere

`\text{Surface area of a hemisphere (A}_1)=\text{ 2}*\pi* r^2`

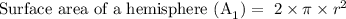
Where

π = 3.14

r= 4.5 inches

Step 2

Write the expression for the surface area of a cone

`\begin{gathered} \text{Surface area of a cone (A}_2)\text{ = }\pi* r* l \\ l\text{ = slant height } \\ To\text{ find l we use Pythagoras theorem} \\ \end{gathered}`

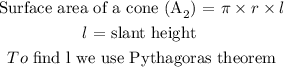
Step 3

Draw the triangle and find l using Pythagoras theorem

From the diagram

l²= 4.5²+10²

l =√(100 + 20.25)

l= √120.25

l = 10.97 inches

Step 4

Find the area of the hemisphere and cone by substitution and calculation

`\begin{gathered} A_{1\text{ }}=2*3.14*4.5^2 \\ A_1=127.17in^2 \\ A_2=\text{ 3.14 }*\text{ 4.5 }*\text{ 10.97} \\ A_2=155.0061in^2 \end{gathered}`

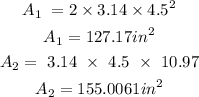
Step 5

Find the total surface area of the shape

`\text{The total surface area of the shape = A}_1+A_2=127.17+155.0061=282.18in^2\text{ approxi}mately`

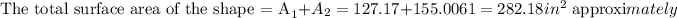
Hence the total area of the shape = 282.2 in²

Option F is the right answer