To find out if the system has a single solution, we have to check wheter its equations are not equivalent to one another and no equation contraticds the others.
If these are some cases, we will find out while we answer, because you will either find an equation that the variable can have any number or we will get to an equation that is wrong for any value of the variable.
To find the solution, we will have to reduce the system to two variable and then to one variable.
To do this, we can pick a variable to get rid of and pair equations so we can achieve this.
Let's get rid of variable y by elimination.
Firstly, we can see that the first equations can by simplifies by dividing it by 3:
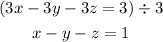
Now, since we want to eliminate y, we need to match its coefficient with another equation, but with opposite sign.
The second equation has a coefficient of -2 on y, so if we multiply the first simplified equation by -2, we will get:
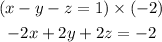
Now, we can add this equation with the second:

Now, we will do similarly but with the last equation. The coefficient of y on it is -4, so we multiply the first simplified equation by (-4):

And add the third equation to it:
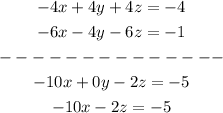
Notice that we can change the sign of all terms on this equation:
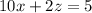
Now, we have two equations and two variable:

However, notice that the left side of the equations are equivalent, because if we multiply the first equation by two, we will get the pair:
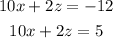
So, the left side is equivalent, but the right sides are different, this means that one equation contradicts the other, That is, there is no possible pair of x and z so that these equations are both true.
This means that there is no solution to this system of equations.