You have the Transfomation:
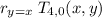
The left part is a reflection in axis y=x
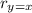
And the right part is a translation
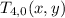
In a transformation in this notation you have to do first the right part and then the left part.
So, in this case to get the initial image ABCD we proceed to the contrary of how it is obtained:
1. We reverse the rotation:
This axis rotation can be represented as follow (y=x):
Then the reverse of the rotation you use the y=x that makes the value of the coordinates:
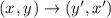
You have this points:
A'' (-4 , 4)
B'' (-1 , 4)
C'' (0, 3)
D'' (- 5, 3)
The reverse rotation will leave the points as follow:
A' (4, -4)
B' (4, -1)
C' (3 , 0)
D' (3 ,-5)
2. Then we reverse the translation of the points A'B'C'D'
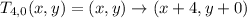
The reverse translation will be:

The initial points (orderer pairs) are:A (0 , -4)B (0 , -1)C (-1 , 0)D ( -1, -5)