SOLUTION
To solve, this problem we will use the sine rule:
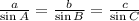
First, let us solve for B, We will relate:
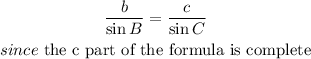
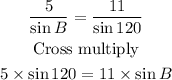

B = 23.2 degrees.
To find A, we will use the sum of angles in a triangle:
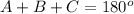
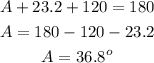
A = 36.8 degrees.
To find a, we will use the sin rule again.
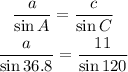
Cross multiply:
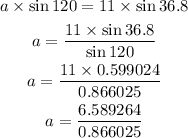
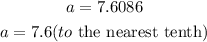
a=7.6
Final answers:
A=36.8 degrees, B=23.2 degrees, a=7.6