ANSWER
r = 3.8
Step-by-step explanation
If AB is tangent to the circle at A, and AO is the radius of the circle, then angle OAB is a right angle. Therefore we have a right triangle:
The hypotenuse of the triangle is segment BO, which by the segment addition postulate is:
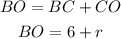
Then we have one leg of the triangle which is AB = 9 and the other leg is r.
Using he pythagorean theorem we can find r:
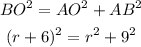
Expanding the binomial on the left side:

Note that we have r² on both sides, so if we subtract r² from both sides:
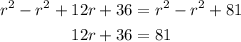
We have a linear equation. Solving for r:
