Solution:
Given:
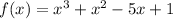
The graph of the function is given below;
The end behavior:
From the graph, the end behavior of the graph shows that as x tends to negative infinity, the function f(x) tends to negative infinity. Also, as x tends to positive infinity, the function f(x) tends to positive infinity.
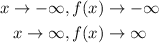
The turning points:
The maximum number of turning points of a polynomial function is always one less than the degree of the function. A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising).

The graph has a maximum and minimum point. Increasing and decreasing, and decreasing and increasing.
Hence, the graph of the function has two turning points.
The number of zeros:
The zeros of a function also referred to as roots or x-intercepts, occur at x-values where the value of the function f(x) = 0.
Hence, the zeros exist at;

Therefore, the function has three zeros.