Start moving constants to the other side of the equation,
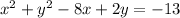
group the x-stuff and y-stuff together,
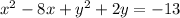
multiply by 1/2 the x-term and the y-term in order to find the missing number in order to complete the squares,
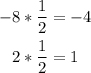
add both terms squared on both sides
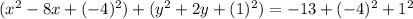
simplify and write as the squared form,
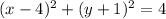
The center of the circle is at (4,-1) and has a radius of 2