Width=10 ft
Lenth=14 ft
Step-by-step explanation
Step 1
Let
length(L)
Width(W)
The length of a rectangle is six feet less than twice the width,it is
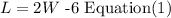
Also, the perimeter of the rectangle is 48,the perimeter is given by:
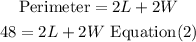
Step 2
using equation (1) and (2), find L and W
a)
replace equation (1) in equation (2)
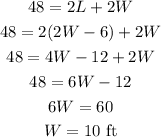
b) replace the value fo W in equation (1) to find L
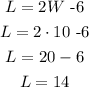
I hope this helps you