Question

A projectile is fired at an angle of 55.0° above the horizontal with an initial speed of 35.0 m/s. How long does it take the projectile to reach the highest point in its trajectory?

Answer 1

We have a projectile that is fired with a initial speed of 35 m/s and an angle of 55 degrees above the horizontal. We want to calculate how long does it take to reach the highest point.

As we are only interested in the vertical trajectory, we will be working with the y-axis.

The vertical speed is equal to the initial speed less the effect of the gravity force. This force is an acceleration that goes against the direction of the vertical initial speed.

We can write this as:

`\begin{gathered} v_y(t)=v_(y0)-g\cdot t \\ v_y(t)=v_o\cdot\sin (\alpha)-g\cdot t \\ v_0=35\text{ m/s} \\ \alpha=55\text{ deg} \\ g=9.8\text{ m/s\textasciicircum 2} \end{gathered}`

The maximum height is reached when the vertical speed is 0. That means that from that time on, the projectile will go downwards.

So we can use the previous formula to solve that for time t:

`\begin{gathered} v_y(t)=0=v_0\cdot\sin (\alpha)-g\cdot t \\ v_0\cdot\sin (\alpha)=g\cdot t \\ t=(v_0\cdot\sin (\alpha))/(g)=(35\cdot\sin (55))/(9.8)=\frac{35\text{ m/s}\cdot0.82}{9.8\text{ m/s\textasciicircum 2}}=2.92\text{ s} \end{gathered}`

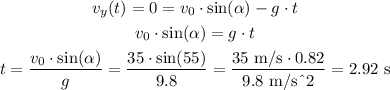
It takes 2.92 seconds for the projectile to reach the maximum height.