Question

Factor differences of square m^4 - n^4

Answer 1

Remember that a difference of squares can be written as the product of two conjugate binomials:

`a^2-b^2=(a+b)(a-b)`

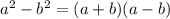
In the given expression, notice that m^4 and n^4 can be written as (m^2)^2 and (n^2)^2:

`m^4-n^4=(m^2)^2-(n^2)^2`

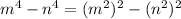
Once written as a difference of squares, we can factor the expression:

`(m^2)^2-(n^2)^2=(m^2+n^2)(m^2-n^2)`

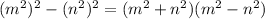
Therefore:

`m^4-n^4=(m^2+n^2)(m^2-n^2)`