Question

Find the slope, x-intercept, and y-intercept for the line 10x-7y + 7 = 0. The slope is The I-intercept is h The y-intercept is Note: Your answers must be decimals. Submit Question Jump to Answer

Answer 1

slope=1.43

y-intercept=1

x-intercept=-1.43

Step-by-step explanation

Step 1

get the slope intercept form of the equation

`y=mx+b\text{ (slope intercept equation)}`

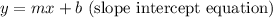
where

m is the slope and b is the y-intercept

to do this, isolate y

`\begin{gathered} 10x-7y+7=0 \\ \text{subtract 10 x in both sides} \\ 10x-7y+7-10x=0-10x \\ -7y+7=-10x \\ \text{subtract 7 in both sides} \\ -7y+7-7=-10x-7 \\ -7y=-10x-7 \\ divide\text{ both sides by -7} \\ (-7y)/(-7)=(-10x)/(-7)-(7)/(-7) \\ y=(10x)/(7)+1 \end{gathered}`

so,

`\begin{gathered} \text{slope}=(10)/(7) \\ y-\text{intercept}=1 \end{gathered}`

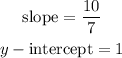
Step 2

to find the x-intercept replace the y value with zero in the equation

`\begin{gathered} y=(10x)/(7)+1 \\ 0=(10x)/(7)+1 \\ \text{subtract 1in both sides} \\ 0-1=(10x)/(7)+1-1 \\ (10x)/(7)=-1 \\ \text{Multiply both sides by 7/10} \\ (10x)/(7)\cdot(7)/(10)=-1\cdot(7)/(10) \\ x=-(7)/(10) \end{gathered}`

so, the x intercept is

`-(7)/(10)`

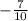
I hope this helps you