Question

Find the point in the first quadrant where the line y = 3x intersects a circle of radius 2 centered at the origin.

Answer 1

We will have the following:

First, we write the both equations: the line and the circle:

`\begin{gathered} y=3x \\ \\ and \\ \\ x^2+y^2=4 \end{gathered}`

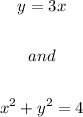
This can be seeing as follows:

Now, we determine the point where the line intersects the circle in the first quadrant, so first, we determine the positive part of the circle, that is:

`\begin{gathered} x^2+y^2=4\Rightarrow y^2=-x^2+4 \\ \\ \Rightarrow y=√(-x^2+4) \end{gathered}`

Now, we equal this expression and the line:

`\begin{gathered} 3x=√(-x^2+4)\Rightarrow(3x)^2=(√(-x^2+4))^2 \\ \\ \Rightarrow9x^2=-x^2+4\Rightarrow10x^2-4=0 \\ \\ \Rightarrow5x^2=2\Rightarrow x^2=(2)/(5) \\ \\ \Rightarrow x=\pm\sqrt{(2)/(5)} \\ \end{gathered}`

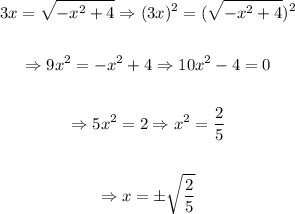
From this, we take the positive value, since it the only one that makes sense under the parameters required, now we find the value of y:

`y=3(\sqrt{(2)/(5)})\Rightarrow y=(3√(10))/(5)`

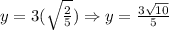
So, the solution is at the point:

`(\sqrt{(2)/(5)}\frac{}{},(3√(10))/(5))`

This can be seeing as follows: