Question

NO LINKS!! Please help me with this problem 3b​

Answer 1

`\textsf{b)} \quad 91.4\% \pm 2.6\%`

Step-by-step explanation:

P-hat is the probability that a given outcome will occur given a specified sample size.

`\boxed{\begin{minipage}{7.5 cm}\underline{P-hat formula}\\\\$\hat{p}=(X)/(n)$\\\\where:\\\phantom{ww}$\bullet$ $\hat{p}$ is the probability. \\ \phantom{ww}$\bullet$ $X$ is the number of occurrences of an event. \\ \phantom{ww}$\bullet$ $n$ is the sample size.\\\end{minipage}}`

Given:

• X = 434
• n = 475

Substitute the given values into the formula to find p-hat:

`\implies \hat{p}=(434)/(475) =0.9136842105...`

The critical value for a 95% confidence level using normal distribution is:

`z=1.9600\;\;\sf (4\;d.p.)`

`\boxed{\begin{minipage}{5.2 cm}\underline{Margin of error}\\\\$ME=z \cdot \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}$\\\\where:\\\phantom{ww}$\bullet$ $z$ is the critical value. \\ \phantom{ww}$\bullet$ $\hat{p}$ is the sample proportion. \\ \phantom{ww}$\bullet$ $n$ is the sample size.\\\end{minipage}}`

Substitute the given values into the margin of error formula:

`\implies ME=1.9600 \cdot \sqrt{((434)/(475)\left(1-(434)/(475)\right))/(475)}`

`\implies ME=0.025255...`

Therefore, an estimate of the proportion of the population of Silvergrove that never attended a rugby match (including a margin of error) is:

`\implies \hat{p}\pm ME`

`\implies 0.914 \pm 0.025`

`\implies 91.4\% \pm 2.5\%`

The final result depends on the accuracy of the z-score and p-hat used in the calculations. As the calculated final result is very close to option B, it can be assumed that the correct answer is option B.

Answer 2

Answer: Choice B)
`\boldsymbol{91.4\%\ \pm \ 2.6\% }`

=======================================================

Step-by-step explanation:

x = number of people who haven't attended a rugby match

x = 434

n = sample size

n = 475

phat = sample proportion of those who haven't attended a rugby match

phat = x/n

phat = 434/475

phat = 0.91368

phat = 91.368%

phat = 91.4%

The goal of the sample statistic phat is to estimate the parameter p, which is the population proportion of those who never attended a rugby match.

-------------------

Your teacher doesn't mention the confidence level, so I'll assume we go for the default of 95%.

At 95% confidence, the z critical value is roughly z = 1.96

Let's compute the margin of error.

E = z*sqrt(phat*(1-phat)/n)

E = 1.96*sqrt(0.91368*(1-0.91368)/475)

E = 0.0252558530311

E = 0.025

E = 2.5%

This is fairly close to the 2.6% margin of error in choice B.

If your teacher uses z = 2 as a rounded estimate of z = 1.96, then,

E = z*sqrt(phat*(1-phat)/n)

E = 2*sqrt(0.91368*(1-0.91368)/475)

E = 0.02577127860317

E = 0.026

E = 2.6%

-------------------

At roughly 95% confidence, the population proportion p is somewhere between
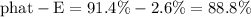`\text{phat} - \text{E} = 91.4\% - 2.6\% = 88.8\%` and
`\text{phat} + \text{E} = 91.4\% + 2.6\% = 94\%`

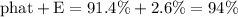
We could write that as this inequality
`88.8\% < p < 94\%`

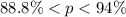
or write it in the format
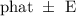`\text{phat} \ \pm \ \text{E}` to get
`\boldsymbol{91.4\%\ \pm \ 2.6\% }`