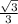#30
We need to find the value of
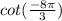
1. We will add 2pi to it until change it from negative to positive, then look for its quadrant
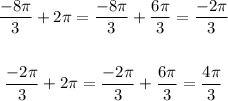
The angle 4pi/3 lies on the 3rd quadrant
Since the angle in the 3rd quadrant has the form
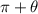
Where theta is an acute angle, then
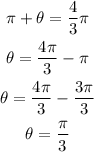
Then we will find the value of tan(pi/3), then reciprocal it to find cot
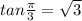
Reciprocal it
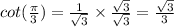
In the 3rd quadrant tan and cot are positive values, then
The value of
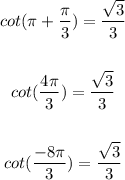
The answer is