The problem can be solved by using the Tangent-Secant Theorem.
The Tangent-Secant Theorem states that if a tangent segment and a secant segment are drawn to a circle from an exterior point, then the square of the measure of the tangent segment is equal to the product of the measures of the secant segment and its external secant segment.
By this definition, we can write out the following expression:
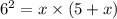
Expanding the expression, we have

The quadratic equation formed can be solved by factorization:
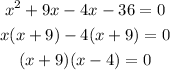
This means that
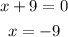
or
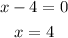
Since the length of the line cannot be negative, the correct value for x is 4.