Question

For each equation chose the statement that describes its solution if applicable give the solution

Answer 1

Isolate the variable from each equation to find the solution. If the algebraic process leads to an identity, all real numbers are solutions. If the algebraic process leads to a contradiction, there is no solution.

Part 1)

`\begin{gathered} 3(u-2)-4u=2(u-9) \\ \\ \Rightarrow\qquad3u-6-4u=2u-18 \\ \\ \Rightarrow\qquad-u-6=2u-18 \\ \\ \Rightarrow\qquad-u-2u=-18+6 \\ \\ \Rightarrow\qquad-3u=-12 \\ \\ \Rightarrow\qquad u=(-12)/(-3) \\ \\ \therefore\quad u=4 \end{gathered}`

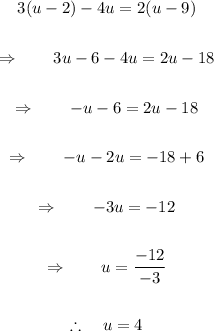
Therefore, the solution is: u=4.

Part 2)

`\begin{gathered} 2(v+1)+4v=3(2v-1)+8 \\ \\ \Rightarrow\qquad2v+2+4v=6v-3+8 \\ \\ \Rightarrow\qquad6v+2=6v+5 \\ \\ \Rightarrow\qquad6v-6v=5-2 \\ \\ \Rightarrow\qquad0=3\;\;! \end{gathered}`

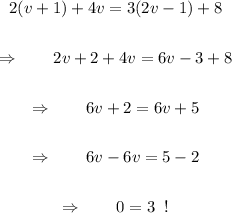
Therefore, there is no solution.