Question

Simplify 1/6+5i to get a complex number in standard a + bi form. Show all of your work.

Answer 1

`(1)/(6+5i)`

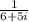
The step in converting this complex number to a + bi form is simply to multiply this complex number by its conjugate. See the solution below.

MTheultiply the expression by the conjugate of the denominator.

`(1)/(6+5i)*(6-5i)/(6-5i)`
`\begin{gathered} =\frac{1(6-5i)}{6(6-5i)+5i(6-5i_{}} \\ =(6-5i)/(36-30i+30i-5i^2) \\ =(6-5i)/(36-5i^2) \\ i^2=-1 \\ =(6-5i)/(36-5(-1)) \\ =(6-5i)/(36+5) \\ =(6-5i)/(41) \\ =(6)/(41)-(5)/(41)i \end{gathered}`

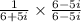
Therefore, its standard form is 6/41 - (5/41)i.