Question

Which of the following logarithmic equations is equivalent to the exponentialequation below? 8^x=512

Answer 1

Given:

The exponential form of the equation is,

`8^x=512`

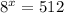
Required:

To find the logarithmic equation equivalent to the given exponential

equation.

Explanation:

We have the given exponential equation as follows:

`8^x=512`

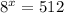
Taking logarithm to the base 8 on both sides of the equation, we get,

`\begin{gathered} \log_88^x=\log_8512 \\ x\log_88=\log_8512 \\ x*(1)=\log_8512 \\ x=\log_8512 \end{gathered}`

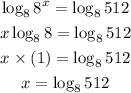
Final Answer:

The logarithmic equation equivalent to the given exponential

equation is,

`x=\log_8512`

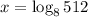
Option B is correct.