Given:
Number of questions = 10
Number of ways = 6
Let's find the different number of ways he can complete the exam.
To find the number of aysm, we are to use the combination formula:
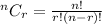
Where:
n = 10
r = 6
Hence, we have:
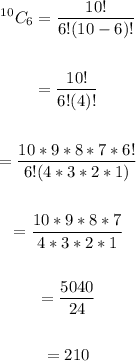
Therefore, the number of ways he can complete the exam is 210 ways.
ANSWER:
210