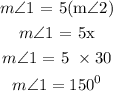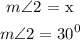ANSWER
Part A:
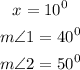
Part B:
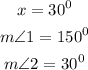
Step-by-step explanation
Part A: Complementary
Two angles are said to be Complementary if there sum is 90 degrees.
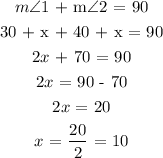
Measure of the two angles
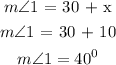
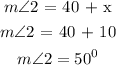
Part B: Supplementary
Two angles are said to be Supplementary if there sum is 180 degrees
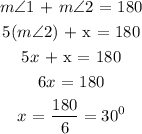
Measure of the two angles