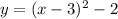Given the equation of a quadratic function in the form:
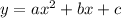
Equation: y = x² - 6x + 7
where a = 1, b = -6, and c = 7.
Vertex form of a quadratic function:
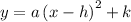
where (h, k) is the vertex.
To find (h, k):
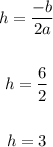
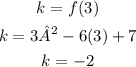
Vertex = (3, -2)
ANSWER
Vertex form of the quadratic equation: