Question

Find the exact length of the midsegment of the trapezoid with the verticesA(2, 0), B(8,-4), C(12, 2), D(0, 10).The length of the midsegment is

Answer 1

First, let's graph the trapezoid.

The midsegment refers to a segment that goes from the midpoint of BC and the midpoint of AD.

Let's find the midpoints using the following formula

`M=((x_1+x_2)/(2),(y_1+y_2)/(2))`
`\begin{gathered} M_(BC)=((8+12)/(2),(-4+2)/(2))=((20)/(2),-(2)/(2))=(10,-1) \\ M_(AD)=((2+0)/(2),(0+10)/(2))=((2)/(2),(10)/(2))=(1,5) \end{gathered}`

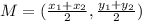
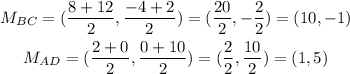
Now, we use the distance formula to find the length of the midsegment

`\begin{gathered} d=\sqrt[]{(y_2-y_1)^2+(x_2-x_1)^2} \\ d=\sqrt[]{(-1-5)^2+(10-1)^2}=\sqrt[]{(-6)^2+(9)^2} \\ d=\sqrt[]{36+81}=\sqrt[]{117} \\ d\approx10.8 \end{gathered}`

Hence, the length of the midsegment is 10.8, approximately.