Given:
Relative speed, v = 0.100 m/s
Mass of satellite 1, m1 = 5.00 x 10³ kg
Mass of satellite 2, m2 = 7.50 x 10³ kg
Assuming that the positive direction is directed from the second satellite towards the first satellite, let's solve for the following:
• (a). Calculate the final velocity after docking, in the frame of reference in which the first satellite was originally at rest.
Apply the Law of Conservation of Momentum:
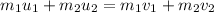
Where:
m1 = 5.00 x 10³ kg
m2 = 7.50 x 10³ kg
u1 is the initial velocity of satellite 1 = 0 m/s
u2 is the initial velocity of satellite 2 = 0.100 m/s
v1 = v2 is the fianl velocity.
This is an inelastic collision.
Thus, we have:
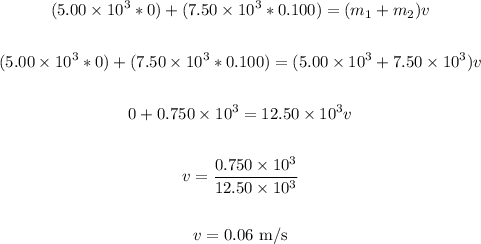
Therefore, the final velocity is 0.06 m/s.
• (b). What is the loss of kinetic energy in this inelastic collision?
Apply the formula:
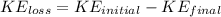
Using the Kinetic Energy formula, we have:
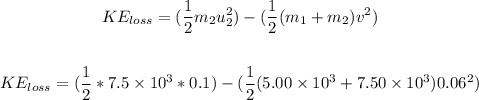
Solving further, we have:
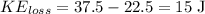
Therefore, the loss of kinetic energy in this inelastic collision is 15 J.
• (c). Let's repeat both parts for which the second satellite was originally at rest.
In this case, we have:
u2 = 0
u1 = 0.1 m/s
Thus, we have:
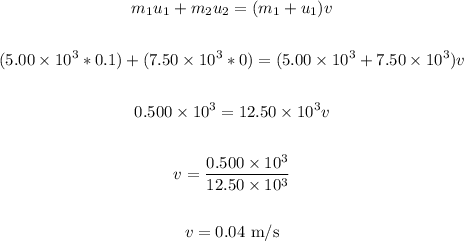
If the second satellite is at rest instead, the final velocity is 0.04 m/s.
• The loss of Kinetic energy:
We have:
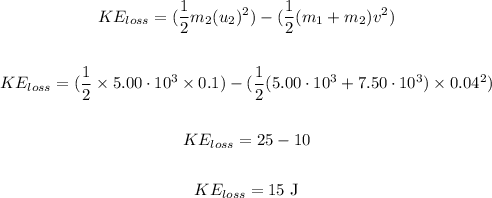
The loss of kinetic energy will be 15 J.
• ANSWER:
(a). 0.06 m/s
(b). 15 J
(c). 0.04 m/s
15 J
There is a change in velocity in the two frames because velocity is relative while the change in kinetic energy is the same in both frames because the Kinetic energy lost to internal forces in a system is always the same regardless of the coordinate system.