Question

Given A=P(1+r)^tFind the annual interest rate if in 2 years an investment of 9,000 grows to 12,960What is the annual rate?

Answer 1

Given the equation:

`A=P(1+r)^t`

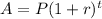
Where A is the final value of an investment, P is the principal (initial investment), t is the time, and r is the annual rate.

We are given:

A = 12,960

P = 9,000

t = 2 years.

It's required to find the value of r.

Substituting into the equation:

`12,969=9,000(1+r)^2`

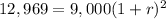
Dividing by 9,000:

`\begin{gathered} (12,960)/(9,000)=(1+r)^2 \\ \\ \text{ Calculating:} \\ \\ (1+r)^2=1.44 \end{gathered}`

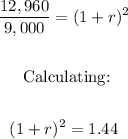
Applying square root on both sides of the equation:

`\begin{gathered} 1+r=√(1.44) \\ \\ 1+r=1.2 \\ \\ r=0.2 \end{gathered}`

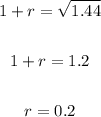
The annual rate is 0.2 * 100 = 20%

r = 20%