Question

17) Given the point A(-3, -2) and B(6, 1), find the coordinates of the point P on directed line segment AB thatpartition AB in the ratio 2:1.

Answer 1

We find the directed line segment AB, as follows:

We subtract the x and y component of the first coordinate from the second one, that is:

`AB=(6-(-3),1-(-2))\Rightarrow AB=(9,3)`

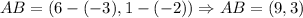
Now, we proceed as follows:

We will use the ratio 2:1 to solve in the following expression to find the x and y coordinates for the point P:

`(x_1+(a)/(a+b)(x_2-x_1),y_1+(a)/(a+b)(y_2-y_1))`

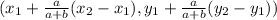
This expression is for a rate of the form a:b.

That is:

`(-3+(2)/(2+1)(6-(-3)),-2+(2)/(2+1)(1-(-2)))=(3,0)`

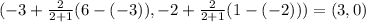
From this, we have that the point p is (3, 0).

***

You can only find the coordinates of the P point by using the formula