Question

Find f and g so that h(x) =(fog) (x). Neither function may be the identity function f(x)=x.
`h(x) = {3}^{ (x)/(2) + 2 }`

Answer 1

If we have that the result of the composition of two functions is the function:

`h(x)=3^{(x)/(2)+2}`

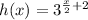
Then, if we have that the function f (x) is:

`3^x`

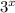
And the function g(x) is:

`g(x)=(x)/(2)+2`

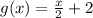
Then, the composition of f(x) and g(x) is:

For the composition of functions, we need to substitute one of the functions in the other function. Then, we have the result for the composition of the functions.