Question

Alex dropped a coin from a height of 240 feet. How long, in seconds, will it take for the object to reach the ground?

Answer 1

Alex dropped a coin from a height of 240 feet.

How long, in seconds, will it take for the object to reach the ground?

This is a free-fall motion and we can use the equations of motion to find out the time.

Recall from the equations of motion,

`h=ut+(1)/(2)gt^2`

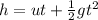
Where h is the height, u is the initial velocity, g is the gravitational acceleration, and t is the time.

We know that the initial velocity is 0 since the coin was at rest before it was dropped.

So, we have the following values

h = 240 feet

u = 0 m/s

g = 9.8 m/s²

Let us substitute these values into the above equation of motion and solve for t

`\begin{gathered} h=ut+(1)/(2)gt^2 \\ 240=(0)t_{}+(1)/(2)(9.8)t^2 \\ 240=(1)/(2)(9.8)t^2 \\ (2\cdot240)/(9.8)=t^2 \\ 48.98=t^2 \\ √(48.98)=t \\ 6.998=t \\ t=7 \end{gathered}`

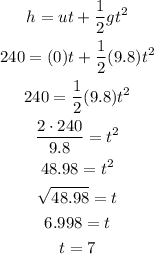
Therefore, it will take 7 seconds for the object to reach the ground.