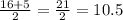To answer this question, we need to sum each of the hours Kevin will practice.
Then, we have that Kevin will practice:
Monday = 1 + 1/2 hours.
Tuesday = 1 + 3/4 hours.
Wednesday = 2 hours.
Next week, Kevin will practice again the same hours:
Monday = 1 + 1/2 hours.
Tuesday = 1 + 3/4 hours.
Wednesday = 2 hours.
On these six days, Kevin will practice:
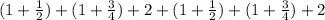
And we can add the whole numbers first:
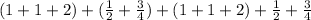
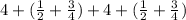
Then, to solve the fractions, we can proceed as follows:
Now, we have:
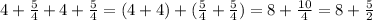
Summing the last two numbers: