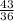Question

4/9 + 3/4 Write your answer as a fraction in simplest form.

Answer 1

We have the following expression:

`(4)/(9)+(3)/(4)`

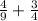
The least commom multiple of 9 and 4 is 36, so we can rewrite our sum as follows:

`(4)/(9)+(3)/(4)=(16+27)/(36)`

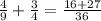
where

`\begin{gathered} 16=(36)/(9)*4 \\ and \\ 27=(36)/(4)*3 \end{gathered}`

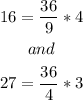
so we have obtained

`(4)/(9)+(3)/(4)=(43)/(36)`

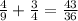
We also can obtaine this result by applying the cross-multiplication rule:

Now, since the number 43 is a prime number, we can not reduce it as a product of other numbers. Then, the simplest fraction form is:

`(43)/(36)`