Answer:
the row in the table closest to the actual solution is x = 0.8
Step-by-step explanation:
Given:
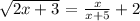
To find:
the row from the table of values is the one closest to the actual solution
Since we were not asked to use a particular method, we will be graphing the equation in order to get the actual solution. Then we will check the table for the row closest to it
Graphing the equation:
From the graph, the solution (point of intersection of both the left-hand side and the right-hand side) is (0.779, 2.135).
The actual solution we need to check for on the table is for x. The x value of the solution from the graph is 0.779
This means our solution is between the row x = 0.7 and x = 0.8
To determine the correct row, we will check for the difference in values of the expressions for x = 0.7 and x = 0.8

Hence, the row in the table closest to the actual solution is x = 0.8