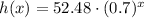Question

Find a formula for the exponential function that satisfies h(3) = 18 and h(6) = 6.174h(x) =

Answer 1

`h(x)=52.48\cdot(0.7)^x^{}`

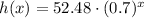
Step-by-step explanation

We have to find the exponential function h(x) such that:

`\begin{gathered} h(3)=18 \\ h(6)=6.174 \end{gathered}`

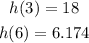
The general form of an exponential function is:

`h(x)=a\cdot b^x^{}`

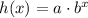
where a = coefficient; b = base

We have to find the values of a and b.

First, substitute x = 3 and h(x) = 18 into the general function:

`18=a\cdot b^3`

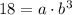
Next, repeat the procedure for x = 6 and h(x) = 6.174:

`6.174=a\cdot b^6`

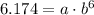
Next, divide the two equations:

`\begin{gathered} \Rightarrow(6.174)/(18)=(a\cdot b^6)/(a\cdot b^3) \\ \Rightarrow0.343=b^(6-3) \\ \Rightarrow b^3=0.343 \end{gathered}`

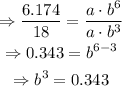
Find the cube root of both sides:

`\begin{gathered} b=\sqrt[3]{0.343} \\ b=0.7 \end{gathered}`

Now, substitute the value of b into the first equation to find a:

`\begin{gathered} 18=a\cdot(0.7)^3 \\ 18=a\cdot0.343 \\ \Rightarrow a=(18)/(0.343) \\ a\approx52.48 \end{gathered}`

Therefore, the formula for the exponential function h(x) is:

`h(x)=52.48\cdot(0.7)^x`