ANSWER:
a. (1, 0)
b. (0, 1/6)
c. x = -2. x = 3
d. y = 0
e. The asymptotes have the form of a line and divide the function into 3 parts.
f.
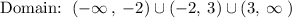
g.

Explanation:
We have the following function:
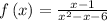
The graph corresponding to the function is the following:
We determine in each case what the statement asks for, like this:
a. the x-intercept(s):

b. the y-intercept:
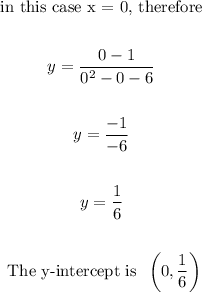
c. the equation(s) of any vertical asymptote(s). The horizontal asymptotes are the values that x cannot take since the function would be discontinuous for those values.
In this case, since it is a rational function, it would be when the denominator is 0, therefore, we solve the following:
![\begin{gathered} x^2-x-6=0 \\ \\ (x-3)(x+2)=0 \\ \\ x-3=0\rightarrow x=3 \\ \\ x+2=0\operatorname{\rightarrow}x=-2 \\ \\ \text{ The equation\lparen s\rparen of any vertical asymptote are:} \\ \\ x=3,x=-2 \end{gathered}]()
d. the equation of the horizontal asymptote. If the degree of the denominator is greater than that of the numerator, the horizontal asymptote is the x-axis, that is:

e. information about the behavior at the asymptote(s).
In this case the behavior of the asymptotes are straight lines that represent values that the function cannot take or cannot reach, divide the function into 3 parts.
f and g.
In this case, the domain is the interval of values that x can take and the range is the interval of values that y can take.
Therefore:
