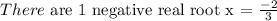Step 1:
Write the polynomial equation
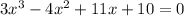
Step 2:
First, find the first factor of the polynomial.
The first factor is 3x + 2
![\begin{gathered} \text{Divide }3x^3-4x^2+11x+10=0\text{ by 3x + 2 using long division} \\ \text{ x}^2\text{ - 2x + 5} \\ 3x\text{ + 2 }\sqrt[]{3x^3-4x^2+11x+10} \\ \text{ -(3x}^3+2x^2) \\ --------------------------- \\ \text{ -6x}^2+11x\text{ + 10} \\ \text{ -}(-6x^2\text{ - 4x)} \\ --------------------------- \\ \text{ 15x + 10} \\ \text{ -(15x + 10)} \\ ---------------------------------- \\ \text{ 0} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/md9mxsebk7qyfyfx04a35c4wcjo4pu7xyy.png)
Step 3
The polynomial
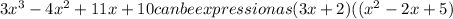
Step 4:
![\begin{gathered} \text{Use the quadratic formula to find the solution to } \\ x^2\text{ - 2x + 5} \\ x\text{ = }\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{a = 1, b = -2 and c = 5} \\ \text{x = }\frac{2\pm\sqrt[]{(-2)^2-4*1*5}}{2*1} \\ \text{x = }\frac{2\pm\sqrt[]{4-20}}{2} \\ \text{x = }\frac{2\pm\sqrt[]{-16}}{2} \\ \text{x = }\frac{2\text{ + 4i}}{2}\text{ , x = }\frac{2\text{ - 4i}}{2} \\ \text{x = 1 + 2i , x = 1 - 2i} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/94m15zalj3xxoyk4zhgh7qvy878zfwm0my.png)
Descartes rule of sign
It tells us that the number of positive real zeros in a polynomial function f(x) is the same or less than by an even number as the number of changes in the sign of the coefficients. The number of negative real zeros of the f(x) is the same as the number of changes in sign of the coefficients of the terms of f(-x) or less than this by an even number.