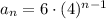Question

If a geometric sequencehas a second term of 24and a fourth term of 384What is the sequence generator?Explain/show your reasoningWrite an equation to represent the sequence.It can be explicit or recursive

Answer 1

We know that the rule for a geometric sequence is given by

`a_n=a_1\cdot r^(n-1)`

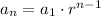
where a_1 is the first term and a_n is the nth term. From the given information, we also know that

`\begin{gathered} n=2\Rightarrow a_2=24 \\ \text{and} \\ n=4\Rightarrow a_4=384 \end{gathered}`

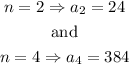
By substituting these values into the geometric sequence formula, we have

`\begin{gathered} 24=a_1\cdot r^(2-1) \\ \text{which gives} \\ a_1\cdot r=24 \end{gathered}`

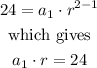
and

`\begin{gathered} 384=a_1\cdot r^(4-1) \\ \text{which gives} \\ a_1\cdot r^3=384 \end{gathered}`

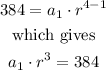
So, we have 2 equations:

`\begin{gathered} a_1\cdot r=24\ldots(i) \\ a_1\cdot r^3=384\ldots(ii) \end{gathered}`

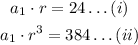
We can express a_1 in term of r by dividing equation (i) by r, that is,

`a_1=(24)/(r)\ldots(iii)`

By substituting this result into equation (ii), we have

`(24)/(r)\cdot r^3=384`

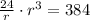
or equivalently,

`24\cdot r^2=384`

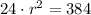
Then by dividing both sides by 24, we have

`\begin{gathered} r^2=(384)/(24) \\ r^2=16 \end{gathered}`

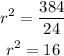
then

`\begin{gathered} r=\sqrt[]{16} \\ r=4 \end{gathered}`

Once we know the result for r, we can substitute its value into equation (iii) and get

`a_1=(24)/(4)=6`

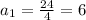
Therefore, the sequence that represents the given values is

`a_n=6\cdot(4)^(n-1)`

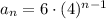
In summary, the answers are:

What is the sequence generator? Answer: The generator is the common ratio r. So, r=4.

Write an equation to represent the sequence. Answer: From our last resul, the equation is

`a_n=6\cdot(4)^(n-1)`