Question

an ordinary fair die is cube with the numbers 1-6 on the sides. imagine that such a die is rolled twice in succession and that the face values of the two rolls are added together. this sum is recorded as the outcome of a single trial of a random experiment. compute the probability of each eventsevent A: the sum is greater than 8event B: the sum is an even numberwrite as a fraction

Answer 1

The table below is the possible outcomes of rolling a fair die twice

First die or first throw is written as row and the second as column.

The total number inside the table is 36. You can try counting it. Also the numbers you have inside is the sums of the throw.

(a) Probability that the sum is greater than 8, we have

The numbers shaded are greater than 8. They are 10 in number out of 36.

Hence the probability is

`\begin{gathered} \frac{possible\text{ outcome}}{\text{total outcome}} \\ (10)/(36) \\ =(5)/(18) \end{gathered}`

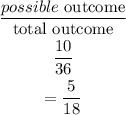
Hence the answer is

`(5)/(18)`

Probability that sum is an even number

The numbers ticked are even numbers. They are 18 in number

Hence probability is

`\begin{gathered} (18)/(36) \\ =(1)/(2) \end{gathered}`

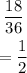
hence the answer is

`(1)/(2)`