Question

How to solve the problem “Compute 3'7 mod 7”

Answer 1

Given

`3^7mod\text{ }7`

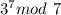
Find

Compute the value of mod

Step-by-step explanation

We have given

`3^7mod\text{ }7`

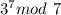
as we can rewrite it

`\begin{gathered} 3^7mod\text{ 7} \\ 2187mod7 \\ \end{gathered}`

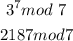
here , we see dividend , a = 2187 and divisor , b = 7

we know ,

`a\text{ mod b = a- \lparen int \lparen a/b\rparen}* b\text{\rparen}`

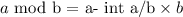
where int is a integer part of the value .

so ,

2187 mod 7 = 2187 -(Int (2187/7)*7)

2187 mod 7 = 2187 - 312 *7

2187 mod 7 = 2187 - 2184

2187 mod 7 = 3

Final Answer

Therefore , the value of 3^7 mod 7 = 3